![]()
二叉树是一种具有层级特性的的数据结构. 这些知识虽说在日常工作中不常使用, 但还是有必要让我们去学习一下, 研究其原理是如何运作. 下面将分享自己的一些理解和学习笔记, 来谈一谈什么是排序二叉树.
二叉树的定义
树(Tree), 是(n>=0)个节点的有限集. 其中 n=0 时, 我们称之为空树. 在一棵非空树中, 只有一个根节点. 在二叉树中, 每个节点最多有两个子节点. 一般称为左节点和右节点(左、右子树).
排序二叉树
二叉排序树(Binary Sort Tree)又称二叉查找树,它是一种特殊的二叉树,它或为空树,或具有以下性质的二叉树:
- 它的右子树非空,则右子树上所有节点的值都大于根节点的值。
- 它的左子树非空,则左子树上所有节点的值都小于根节点的值。
- 左右子树各是一颗二叉排序树。
构建排序二叉树
二叉树大多也是递归定义的. 下面根据排序二叉树的特性来创建一个二叉树.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
| function BinaryTree(key) {
var root = null;
var Node = function(key) {
this.key = key;
this.left = null;
this.right = null;
};
var insertNode = function(node, newNode) {
if (newNode.key < node.key) {
if (node.left === null) {
node.left = newNode;
} else {
insertNode(node.left, newNode);
}
} else {
if (node.right === null) {
node.right = newNode;
} else {
insertNode(node.right, newNode);
}
}
};
this.insert = function(key) {
var newNode = new Node(key);
if (root === null) {
root = newNode;
} else {
insertNode(root, newNode);
}
};
}
var nodes = [8, 3, 10, 1, 6, 14, 4, 7, 13];
var binaryTree = new BinaryTree();
nodes.forEach(function(key) {
binaryTree.insert(key);
});
|
遍历二叉树
我们已经构建好了一个排序二叉树, 现在想要获取二叉树每一个节点的信息, 因此我们需要遍历节点, 对它做一些操作.
中序遍历
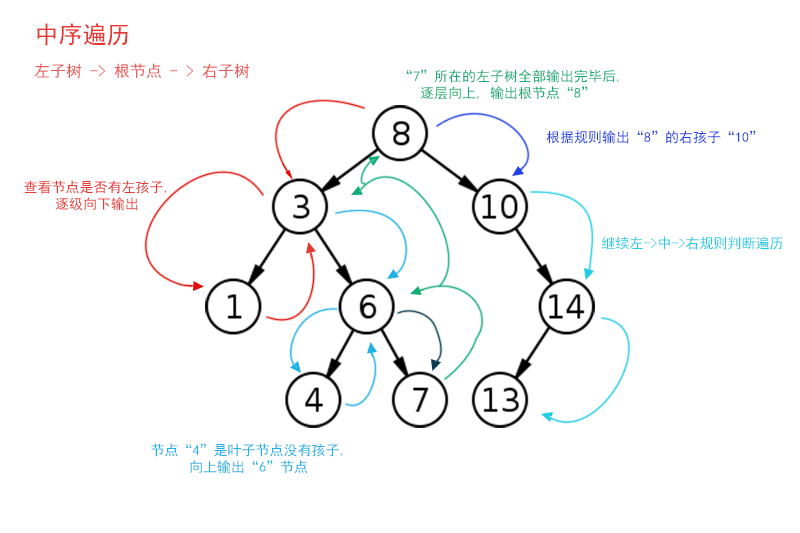
二叉树有三种遍历的方法, 分别是中序遍历, 前序遍历, 后序遍历. 其中中序遍历的顺序是: 左子树 -> 根元素 -> 右子树.
对于二叉排序树来说,中序遍历得到的序列是一个从小到大排序好的序列. 百闻不如一见, 我们先看看图中的路线图, 整理一下思路先.
![]()
这里我们需要加入中序遍历的接口, 因此我们在原先代码上继续扩展并运行.
控制台会依次输出”1 3 4 6 7 8 10 13 14”
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
| function BinaryTree(key) {
var root = null;
var Node = function (key) {
this.key = key;
this.left = null;
this.right = null;
}
var insertNode = function (node, newNode) {
// 对比新旧节点
if (newNode.key < node.key) {
// 左节点是否存在
if (node.left
node.left = newNode;
} else {
insertNode(node.left, newNode);
}
} else {
if (node.right
node.right = newNode;
} else {
insertNode(node.right, newNode);
}
}
}
+ // 中序遍历
+ var inOrderTraverseNode = function (node, callback) {
+ // 递归遍历, 当到最后叶子节点时, 下面没有节点就会直接返回
+ if (node !== null) {
+ inOrderTraverseNode(node.left, callback);
+ callback(node.key);
+ inOrderTraverseNode(node.right, callback);
+ }
+ }
// 插入节点
this.insert = function (key) {
var newNode = new Node(key)
if (root
root = newNode;
} else {
insertNode(root, newNode);
}
}
+ /**
+ * 中序遍历
+ * @param {Function} callback - 决定如何处理节点
+ */
+ this.inOrderTraverse = function (callback) {
+ inOrderTraverseNode(root, callback);
+ }
+ }
// 初始化调用
var nodes = [8, 3, 10, 1, 6, 14, 4, 7, 13]
var binaryTree = new BinaryTree();
nodes.forEach(function (key) {
binaryTree.insert(key)
})
+ // 调用成功后输出当前节点
+ var callback = function (key) {
+ console.log(key)
+ }
// 中序调用
+ binaryTree.inOrderTraverse(callback);
|
前序遍历
虽然前面已经有了中序遍历可以遍历节点, 为啥还要浪费精力学前序呢? 诶~这是因为每一种遍历都有自己应用优势.
前序遍历最大的作用, 就是如果我们想把已经有了的二叉树重新复制一遍, 使用前序遍历得到的效率相比重新构造一次来说, 两者的差距能差好几倍.
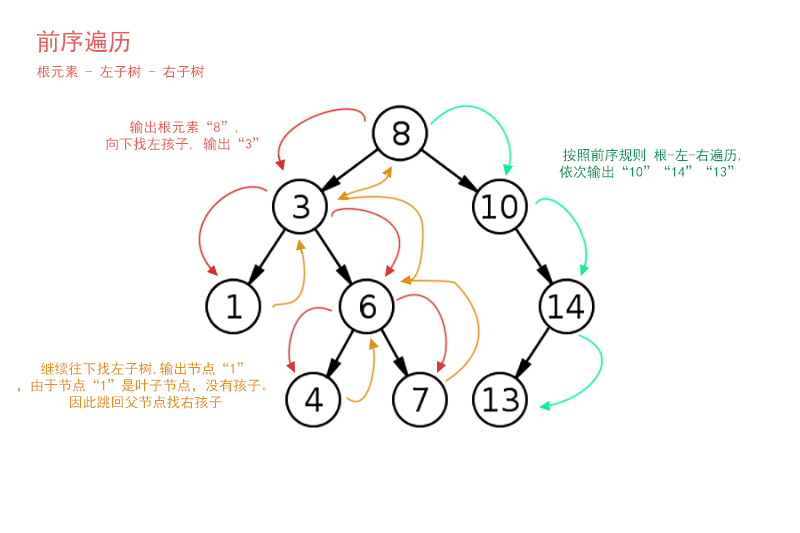
前序遍历的顺序与中序遍历有些不同, 前序是以: 根元素 - 左节点 - 右节点的顺序来遍历.
![前序遍历路线图]()
这里将遍历的路线图简化了下, 红色输出, 黄色返回上一级, 而绿色则是右子树遍历. 可以看到这是很典型的递归思想. 紧接着我们继续在代码上进行扩展.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
| function BinaryTree(key) {
var preOrderTraverseNode = function (node, callback) {
if (node !== null) {
callback(node.key)
preOrderTraverseNode(node.left, callback)
preOrderTraverseNode(node.right, callback)
}
}
this.preOrderTraverse = function (callback) {
inOrderTraverseNode(root, callback);
}
binaryTree.preOrderTraverse(callback);
}
|
后序遍历
看到这里, 大家可能已经意识到了. 不同的遍历方法实际上是对当前的节点访问的顺序不一样. 后序遍历的访问的次序就是: 左节点 - 右节点 - 根元素. 它的特点是, 当下面的左右孩子都遍历完了后才会触发回调函数(callback). 因此适用于破坏性操作的情况, 比如删除所有的节点
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
| function BinaryTree(key) {
var preOrderTraverseNode = function (node, callback) {
if (node !== null) {
preOrderTraverseNode(node.left, callback)
preOrderTraverseNode(node.right, callback)
callback(node.key)
}
}
this.postOrderTraverseNode = function (callback) {
inOrderTraverseNode(root, callback);
}
binaryTree.postOrderTraverse(callback);
}
|
二叉树节点查找
找出排序二叉树的最大节点和最小节点实际上也很简单. 前文提过, 根据排序二叉树的特性, 节点左孩子的值, 一定比节点本身小. 节点右孩子的值一定比节点本身大. 因此我们可以根据这个规则来进行查找:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
| function BinaryTree(key) {
var minNode = function (node) {
if (node) {
while (node && node.left !== null) {
node = node.left;
}
return node.key;
}
return null;
}
var maxNode = function (node) {
if (node) {
while (node && node.right) {
node = node.right;
}
return node.key;
}
return null;
}
this.min = function () {
return minNode(root)
}
this.max = function () {
return maxNode(root)
}
}
console.log("min node is:" + binaryTree.min())
console.log("min node is:" + binaryTree.max())
|
查找节点是否存在:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
| function BinaryTree(key) {
var searchNode = function (node, key) {
if (!node) return false
if (key < node.key) {
return searchNode(node.left, key)
} else if (key > node.key) {
return searchNode(node.right, key)
} else {
return true
}
}
this.search = function (key) {
return searchNode(root, key)
}
}
console.log(binaryTree.search(7) ? "key 7 is found" : "key 7 is not found")
console.log(binaryTree.search(9) ? "key 9 is found" : "key 9 is not found")
|
总结
最后将上面的知识总结一下. 首先知道了树的实际上是一种具有层级特性的数据结构, 其中排序二叉树又是一种特殊的树. 它的具有以下几种性质:
- 如果左(孩子)子树不为空, 那么左子树一定比父节点(根节点)的值小.
- 如果右(孩子)子树不为空, 那么右子树一定比父节点(根节点)的值大.
- 其中左、右子树也分别是排序二叉树.
紧接着创建了二叉树节点后, 我们需要去遍历这些节点. 遍历的方法又分前序遍历, 中序遍历, 后序遍历. 三者的区别仅在遍历的顺序不同, 但却有着不同优势.
- 前序遍历是唯一一个从根元素开始遍历的, 其顺序为 根 - 左 - 右, 由于它是从根左右开始, 非常适合像复制节点这样的工作.
- 中序遍历的顺序是 左 - 根 - 右, 返回的是一个从小到大(从大到小)排序的好序列.
- 后序遍历的顺序是 左 - 右 - 根, 其特点是执行操作时,肯定已经遍历过该节点的左右子节点,故适用于要进行破坏性操作的情况,比如删除所有节点.
后面还讲到了二叉树节点查找, 利用递归找到二叉树中最小(大)的节点值等.
数据结构的学习之路还很长, 以后再一点一点慢慢的深入吧~